Optimizate The Branched Lightguide Using Rayzen Software

1. Background Introduction

The design of light collection systems and light guiding systems is a critical component of optical system design. The primary goal of the light collection system design is to improve the transmission efficiency of light energy and reduce losses caused by reflection, scattering, and absorption during the transmission process. The main objectives of light guiding system design are to deliver light energy to the desired location and to enhance the transmission efficiency and uniformity of the light distribution.

A branched lightguide is a common type of light collection system that can evenly distribute light energy among multiple lightguides, thereby improving the transmission efficiency of light energy. This optical structure can be used for lighting applications in basements or subway stations by introducing natural light indoors throughout its path, significantly reducing energy consumption and contributing positively towards achieving green lighting and carbon neutrality goals. In automotive dashboards, branched lightguides can allocate the energy from a central light source to various indicator lights or displays, reducing the need for separate wiring.

This article employs Rayzen software to optimize the branched lightguide system, aiming to achieve efficient light energy transmission and minimize light energy loss.

2. Performance Metrics

The performance metrics for light collection and guiding systems primarily include light energy transmission efficiency and uniformity upon reaching the target position. In Rayzen software, these performance metrics can be evaluated through the following parameters:

Light Energy Transmission Efficiency: Measured by calculating the power received at two receivers; a higher value indicates better light energy transmission efficiency. Given that this case involves a planar symmetric structure, we only need to calculate the power at one receiver. The target value is set to 0.5 when the relative power of the light source is 1W.
Uniformity: Assessed by evaluating the light intensity distribution at the target position as received by the two receivers. A more uniform distribution indicates better uniformity, which can be quantified using the standard deviation of the light intensity distribution on the receiver. The target value for uniformity is 0.0.

Based on the above metrics, an evaluation function is constructed as follows: $MF = \omega_1 \cdot \text{abs}(P - 0.5) + \omega_2 \cdot (\text{std} - 0.0)$ where $\omega_1$ and $\omega_2$ are the weights for the two metrics (defaulted to 1), $\text{P}$ represents the power received at the receiver, and $\text{std}$ denotes the standard deviation of the light intensity distribution on the receiver.

3. Optimization Process

Rayzen software is utilized to optimize the branched lightguide system to achieve efficient light energy transmission and uniform light distribution at the output positions. The optimization process follows the outlined steps in Figure [1].

Figure [1]. Optimization Procedure.

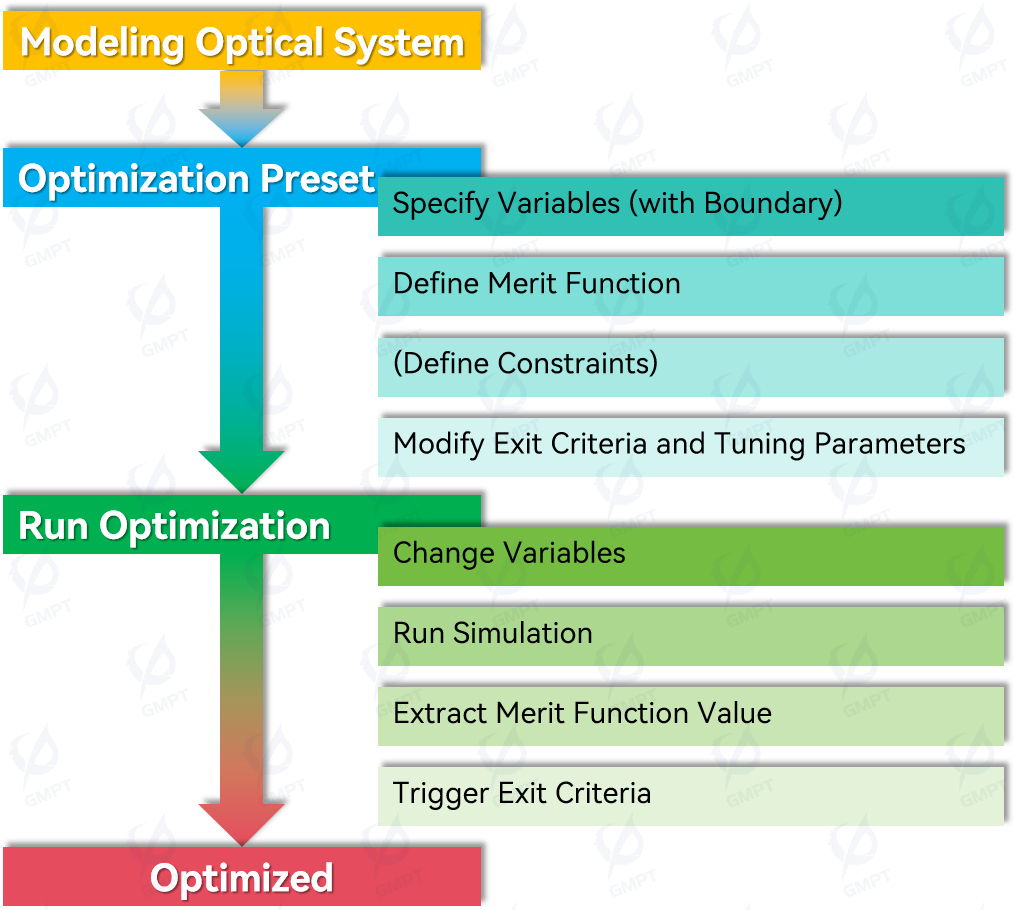
4. Model Construction

As illustrated in Figure [2], the branched lightguide system consists of a point light source with a divergence angle of 30°, two flat receivers located on either side of the lightguide, and a material composition of PMMA for the lightguide. Light travels within the lightguide via total internal reflection and is eventually collected at the receivers. The lightguide comprises an entrance port, two quarter-circle bends, and two lightguide arms, all joined together through Boolean operations. Each time the radius and arm length are modified, the interdependencies between model parameters must be considered. Using the scripting modeling feature in Rayzen software facilitates defining parameter constraints, simplifying subsequent optimization calculations.

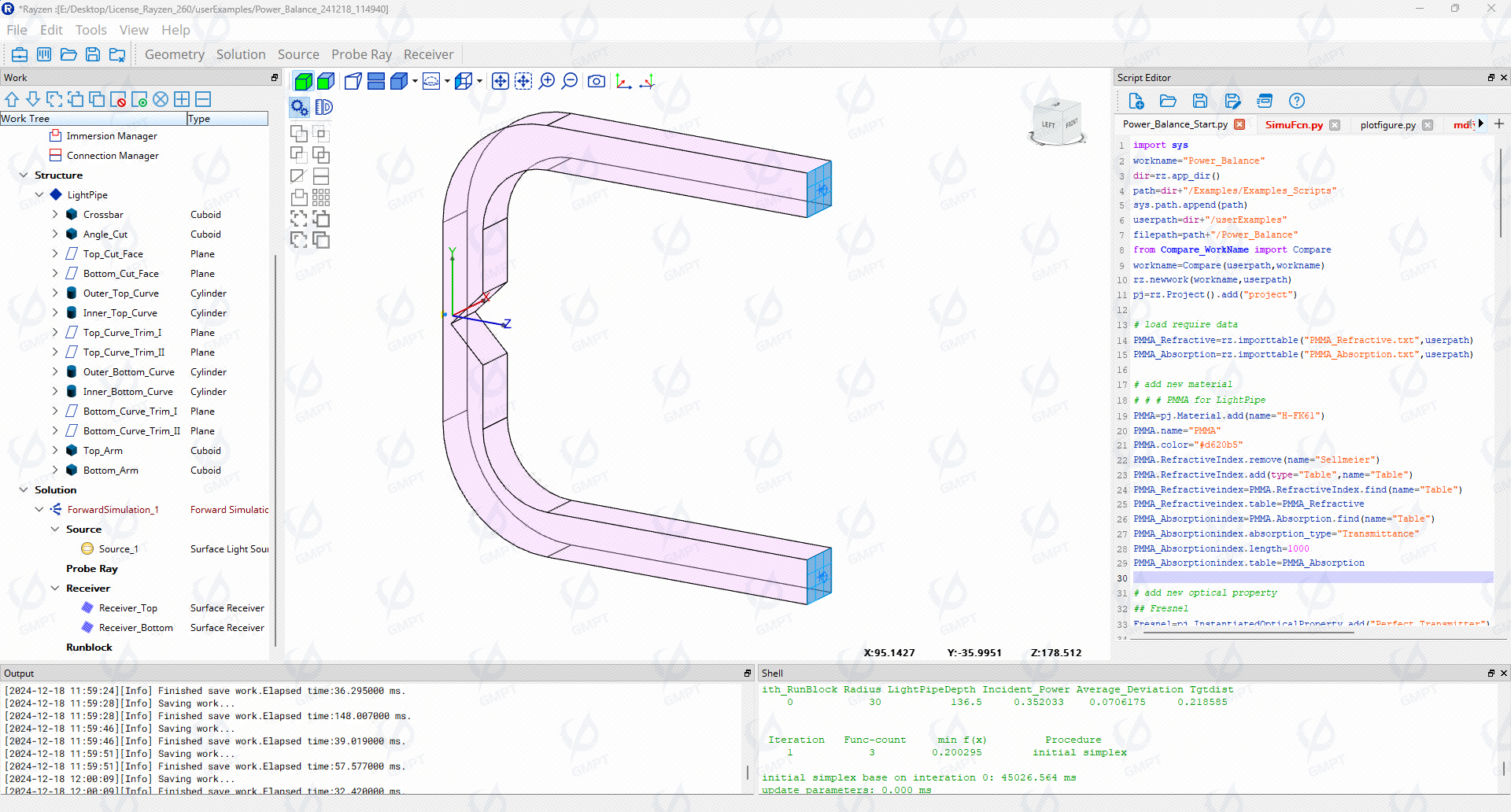
Figure [2]. Schematic of Branched Lightguide

5. Optimization Model and Parameter Settings

In this case, the Nelder-Mead simplex algorithm is employed to optimize the curvature radius and arm length of the lightguide. The Nelder-Mead simplex method is a numerical optimization technique used to find the minimum of a function in multidimensional space without relying on gradient information, making it suitable for problems where gradients are difficult to compute or define.

The algorithm starts by constructing an initial simplex based on given initial guesses. By slightly altering each dimension of the initial guess, additional vertices are created to form an $n + 1$ -vertex simplex in $n$ -dimensional space. Through iterations, the algorithm adjusts the simplex's position toward the optimal solution using operations such as reflection, expansion, contraction, and shrink until convergence criteria are met.

1. Reflection

Improvement Basis: When the objective function value at the reflection point $x_{r}$ is better than that of the worst point but not as good as the best point, it indicates that the simplex can be improved by this new point. The reflection operation aims to find a better position by "mirroring" the worst point about the centroid of the remaining points.

$x_r = x_{\text{bar}} + \alpha (x_{\text{bar}} - x_{\text{worst}})$

Here, $x_{\text{bar}}$ represents the average position of all points except the worst point, and $\alpha > 0$ is the reflection coefficient, with a default value of 1.

2. Expansion

Improvement Basis: If the objective function value at the reflection point $x_{r}$ is exceptionally good, even better than the current best point, further exploration along the reflection direction can be attempted to find an even better point. This accelerates the convergence process towards the optimal solution.

$x_e = x_{\text{bar}} + \gamma (x_r - x_{\text{bar}})$

Here, $\gamma > 1$ is the expansion coefficient, with a default value of 2.

3. Contraction

Improvement Basis: If the performance of the reflection point $x_{r}$ is poor, meaning its objective function value is not better than the worst point, a more conservative approach is necessary. Contraction operations come in two types:

Outside Contraction: Used when the reflection point lies between the worst and second-worst points. $x_c = x_{\text{bar}} + \beta (x_r - x_{\text{bar}})$
Inside Contraction: Used when the reflection point is worse than the worst point. In this case, the contraction point moves closer to the centroid to avoid excessive deviation from the potentially optimal region. $x_c = x_{\text{bar}} + \beta (x_{\text{worst}} - x_{\text{bar}})$

Here, $0 < \beta < 1$ , with a typical default value of 0.5.

4. Shrink

Improvement Basis: When none of the above three operations effectively improve the simplex, it suggests that the simplex may have enclosed a local minimum or encountered difficulties. The shrink operation moves all vertices toward the best point, helping to reshape the simplex for better adaptation to the new search space.

$x_i = x_{\text{best}} + \sigma (x_i - x_{\text{best}}), \quad i = 1, ..., n+1$

Here, $0 < \sigma < 1$ , with a typical default value of 0.5.

6. Optimization Results and Analysis

6.1 Mechanism Analysis

We begin with theoretical analysis to understand the relationship between variables and evaluation metrics, providing a theoretical basis for the optimization direction.

Receiver Power vs Radius: Receiver power should increase as the radius grows because too small a radius would cause excessive bending of the lightguide, leading to significant light leakage due to unsatisfied total internal reflection conditions.
Standard Deviation vs Arm Length: The standard deviation of light intensity distribution on the receiver should decrease as the arm length increases and gradually stabilize. This behavior is consistent with the principle of light mixing rods (匀光棒), where light rays entering at different angles undergo multiple total internal reflections. Each reflection creates a new virtual light source image, and these images are superimposed. As the length of the light guide increases, light rays have more opportunities to reflect, which enhances the mixing of light from different directions and thus improves light uniformity. Occasionally, specific periodic conditions may form within the optical path, causing the uniformity to increase in an oscillatory manner as the length increases.
Receiver Power vs Arm Length: Receiver power should decrease as the arm length increases due to absorption and scattering effects within the material. As the arm length grows, the propagation distance of light within the material also increases, leading to more light being absorbed and scattered, thereby reducing the received power. For materials with high transmittance, this effect might not be significant and therefore is not considered a primary factor in the direction of thought.
Standard Deviation vs Radius: There is no clear direct association between the standard deviation of light intensity distribution on the receiver and the radius, making it challenging to parse their intrinsic connection from a physical perspective. In optimization design, we focus on factors with explicit causal relationships and predictable impacts to ensure the effectiveness and reliability of the optimization process.

6.2 Parameter Scanning

If the initial values are good enough, the optimization method can quickly converge to the global optimum. Poor initial values, however, may lead to local optima rather than the global optimum. Therefore, if feasible, parameter scanning is conducted to identify sufficiently good initial values, allowing the simplex method to more rapidly locate the global optimum.

Figure [3] illustrates the trend of receiver power versus radius over iteration counts, showing that receiver power increases with radius, particularly after exceeding 40mm, indicating slower growth. This aligns with theoretical analysis, suggesting selecting a radius of 40mm as an initial value for faster convergence.

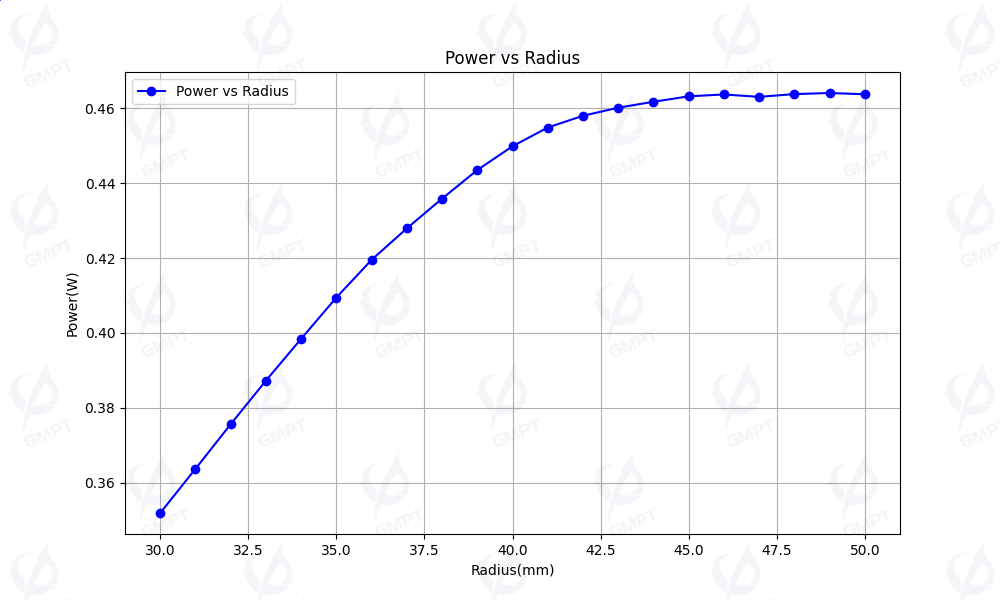
Figure [3]. Parameter Scanning：Receiver Power vs Radius

Figure [4] shows the trend of the standard deviation of light intensity distribution on the receiver versus arm length over iteration counts, demonstrating that the standard deviation decreases oscillatingly as arm length increases and stabilizes after surpassing 140mm. This supports theoretical analysis, recommending an initial arm length of 140mm for quicker convergence.

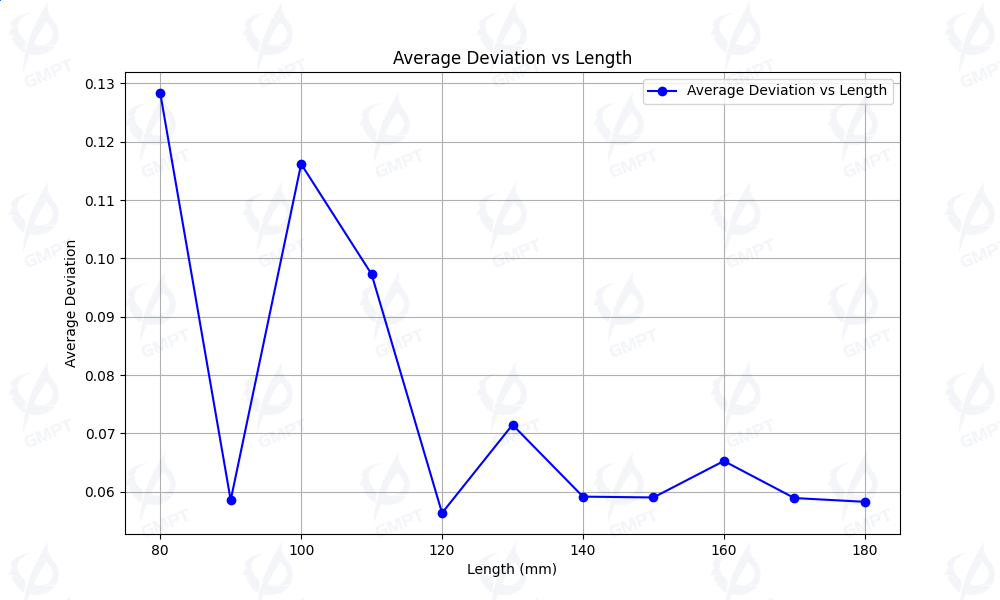
图 [4]. Parameter Scanning：Standard Deviation vs Arm Length

6.3 Simplex Optimization

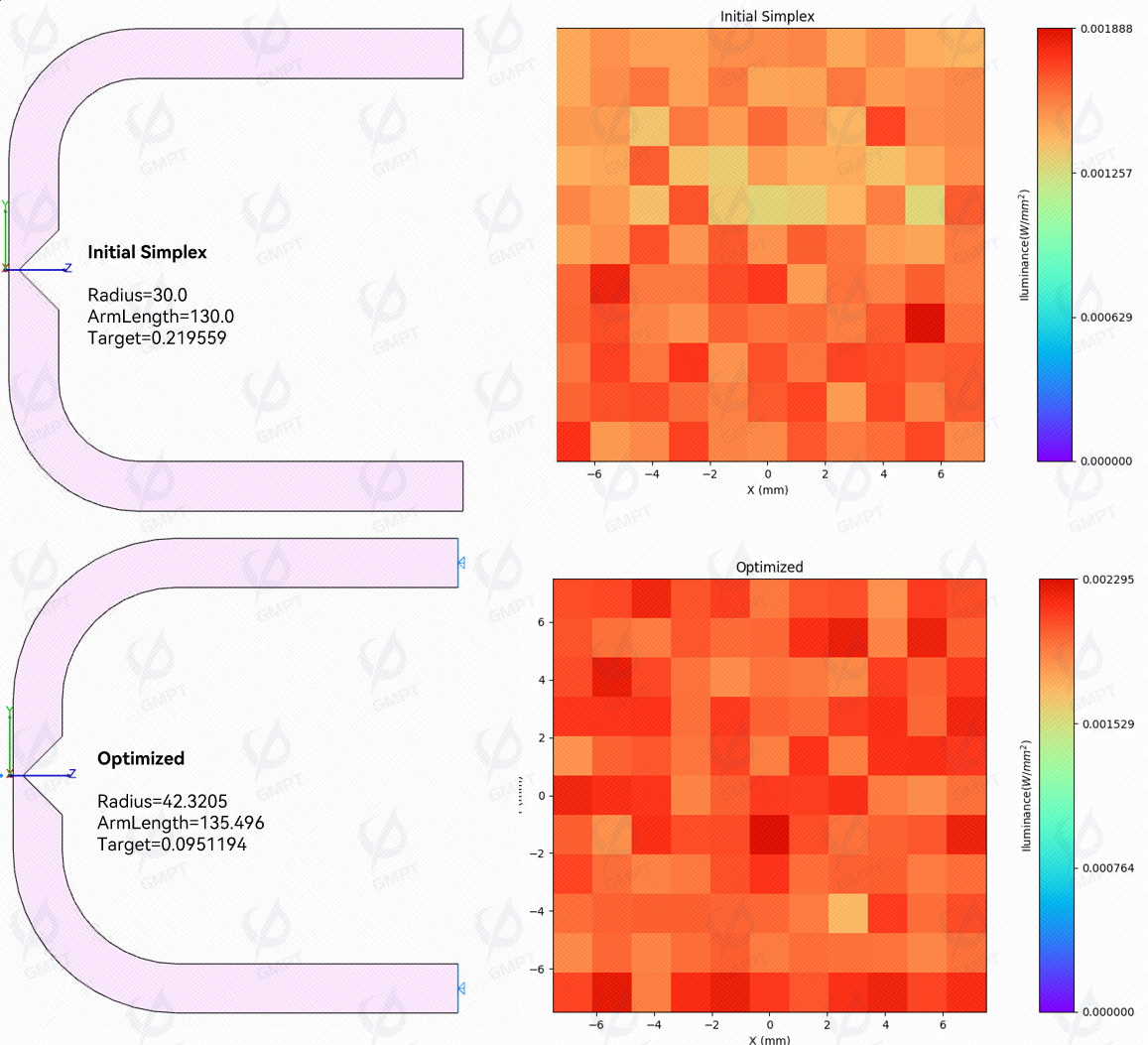
Figure [5] depicts the process of optimizing the branched lightguide system without selecting initial values, starting from a radius of 30mm and an arm length of 130mm. After 15 iterations, the evaluation function tends to converge, meeting the convergence criterion by the 32nd iteration.

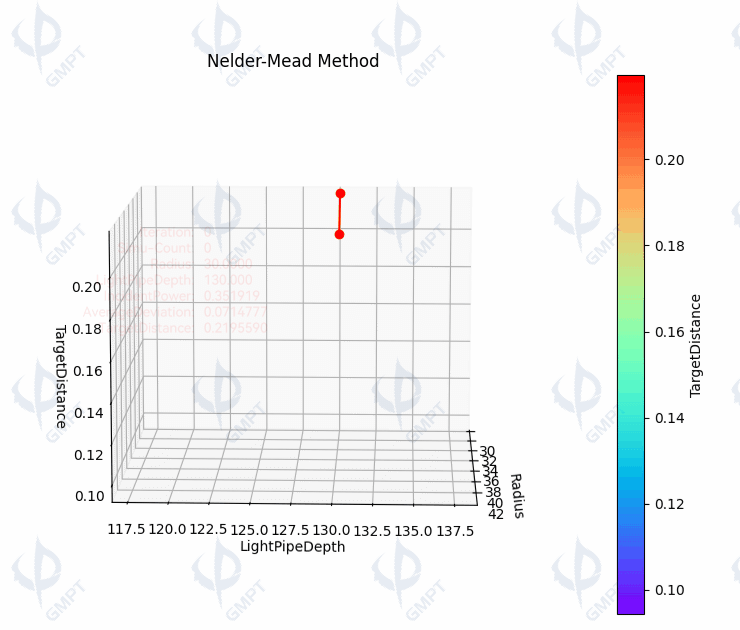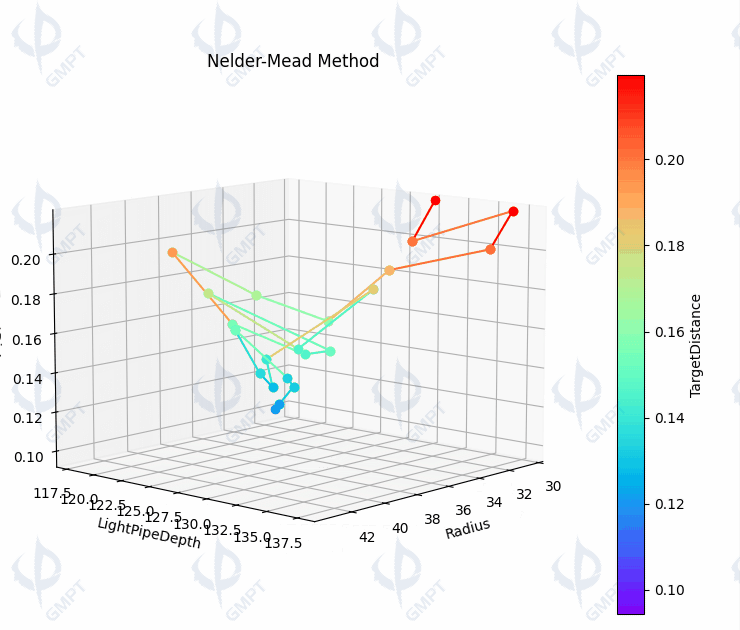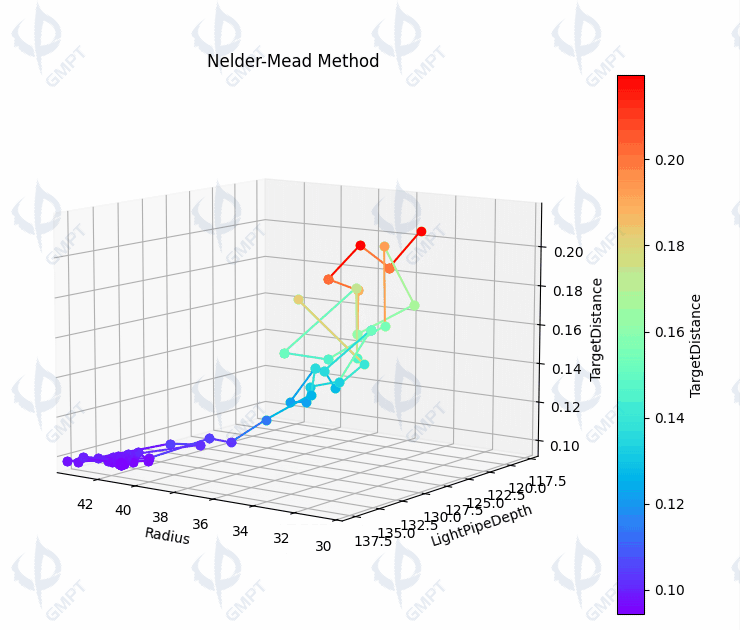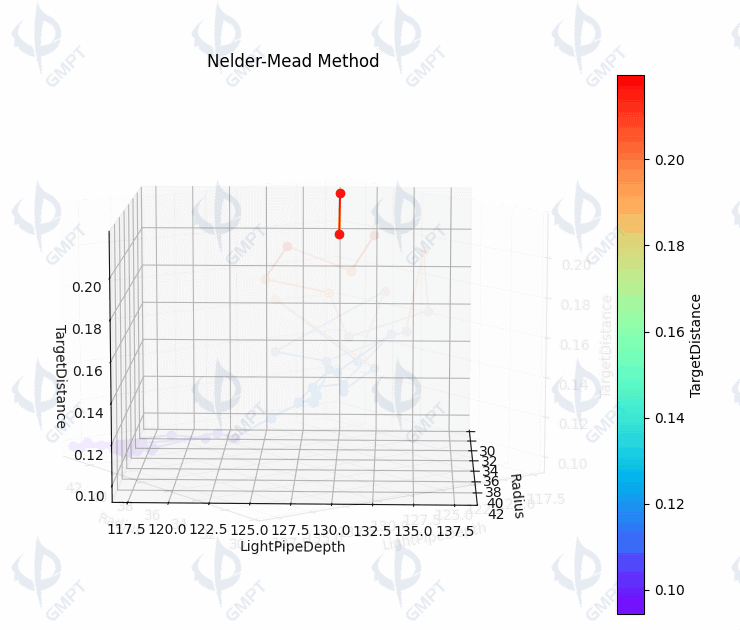
Figure [5]. The descent process of merit function optimized by simplex method

Figure [6] compares the structure and illuminance distribution on the receiver before and after optimization, revealing increased light energy reception and more uniform light intensity distribution on the receiver post-optimization, thereby enhancing the performance of the branched lightguide system.

Figure [6]. Comparison of structure and receiver illumination distribution before and after optimization

7. Conclusion and Outlook

This article uses Rayzen software to optimize the curvature radius and arm length of the lightguide via the Nelder-Mead simplex method, resulting in an optimal design scheme. Through theoretical analysis, we determined the parameters for scanning and selected appropriate initial values to provide a theoretical basis for the optimization direction. The optimization results are consistent with theoretical analyses, demonstrating that the optimized branched lightguide system achieves higher receiver power and more uniform light intensity distribution, thereby enhancing system performance. For this specific case, due to the monotonic nature of the parameter space, the gradient descent method could have found the global optimum more quickly. However, the simplex method offers a more robust approach for cases with unclear parameter spaces. Future work will explore other optimization algorithms, such as genetic algorithms and particle swarm optimization, in conjunction with various other optical systems for simulation and design, offering richer design concepts to the industry.