Simulation and Design of Super Junction VDMOS Devices Using Nuwa TCAD Software

GMPT, October 2024

Abstract: Vertical Double-Diffused Metal Oxide Semiconductor Field Effect Transistor (VDMOS) is a unipolar power switching device with advantages of fast switching speed and high static input impedance. It is widely used in motor speed control, radar, switching power supplies, automotive electronics, inverters, and mobile communication. Super-junction VDMOS introduces a super-junction structure based on traditional VDMOS, replacing the lightly doped structure in the drift region. When the device is in a reverse-biased state, under the influence of the transverse electric field, the charges of the N-type semiconductor and P-type semiconductor in the super-junction region are mutually compensated and depleted, forming a transverse voltage-sustaining layer and enhancing the device’s reverse breakdown voltage.

This article presents the simulation of a super-junction VDMOS device using Nuwa TCAD software and showcases the simulation results.

1. Device Structure

Figure 1. Schematic of Super-junction VDMOS Device Structure

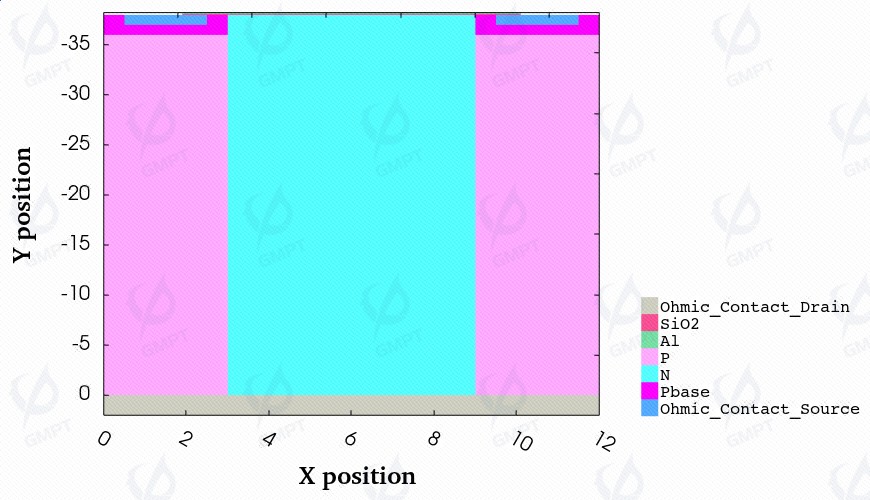
In this work, the super-junction VDMOS device structure is shown in Figure 1. The P-pillar height is set to 36 μm, the cell width is set to 12 μm, and the doping concentrations are set as follows: pillar region at $2\times 10^{15}{\text{cm}}^{-3}2\backslash times\; 10^\{15\}\; \backslash text\{cm\}^\{-3\}$, P-base region at $5\times 10^{16}{\text{cm}}^{-3}5\backslash times\; 10^\{16\}\; \backslash text\{cm\}^\{-3\}$, drain region at $5\times 10^{19}{\text{cm}}^{-3}5\backslash times\; 10^\{19\}\; \backslash text\{cm\}^\{-3\}$, and source region at $1\times 10^{18}{\text{cm}}^{-3}1\backslash times\; 10^\{18\}\; \backslash text\{cm\}^\{-3\}$. The gate oxide thickness is set to 0.1 μm. (Some simulation data in this article are sourced from reference [1].)

2. Physical Model Settings

2.1 Continuity Equations

$$\begin{array}{cccc}& {\displaystyle \mathrm{\nabla }\cdot J_n-\sum _j{R}_n^{tj}-R_{sp}-R_{st}-R_{au}+G_{opt}(t)=\frac{\mathrm{\partial }n}{\mathrm{\partial }t}+N_D\frac{\mathrm{\partial }{f}_D}{\mathrm{\partial }t}}& & \end{array}\backslash begin\{align\}\; \backslash nabla\; \backslash cdot\; J\_n-\backslash sum\_j\; R\_n^\{t\; j\}-R\_\{s\; p\}-R\_\{s\; t\}-R\_\{a\; u\}+G\_\{o\; p\; t\}(t)=\backslash frac\{\backslash partial\; n\}\{\backslash partial\; t\}+N\_D\; \backslash frac\{\backslash partial\; f\_D\}\{\backslash partial\; t\}\; \backslash end\{align\}$$ $$\begin{array}{cccc}& {\displaystyle \mathrm{\nabla }\cdot J_p+\sum _j{R}_p^{tj}+R_{sp}+R_{st}+R_{au}-G_{opt}(t)=-\frac{\mathrm{\partial }p}{\mathrm{\partial }t}+N_A\frac{\mathrm{\partial }{f}_A}{\mathrm{\partial }t}}& & \end{array}\backslash begin\{align\}\; \backslash nabla\; \backslash cdot\; J\_p+\backslash sum\_j\; R\_p^\{t\; j\}+R\_\{s\; p\}+R\_\{s\; t\}+R\_\{a\; u\}-G\_\{o\; p\; t\}(t)=-\backslash frac\{\backslash partial\; p\}\{\backslash partial\; t\}+N\_A\; \backslash frac\{\backslash partial\; f\_A\}\{\backslash partial\; t\}\; \backslash end\{align\}$$

2.2 Poisson Equation

$$-\mathrm{\nabla }\cdot \left(\frac{{ϵ}_0{ϵ}_{dc}}{q}\mathrm{\nabla }V\right)=-n+p+N_D(1-f_D)-N_A{f}_A+\sum _j{N}_{tj}({\delta }_j-f_{tj})-\backslash nabla\; \backslash cdot\backslash left(\backslash frac\{\backslash epsilon\_0\; \backslash epsilon\_\{d\; c\}\}\{q\}\; \backslash nabla\; V\backslash right)=-n+p+N\_D\backslash left(1-f\_D\backslash right)-N\_A\; f\_A+\backslash sum\_j\; N\_\{t\; j\}\backslash left(\backslash delta\_j-f\_\{t\; j\}\backslash right)$$

2.3 Low-Field and High-Field Mobility Models

• Low-Field Mobility Model (Masetti Model):

  $${\mu }_0={\mu }_{\min 1}{e}^{-\frac{P_c}{N_i}}+\frac{{\mu }_{\max }{\left(\frac{T_L}{T_0}\right)}^{-\zeta }-{\mu }_{\min 2}}{1+{\left(\frac{N_i}{C_r}\right)}^{\alpha }}-\frac{{\mu }_1}{1+{\left(\frac{C_s}{N_i}\right)}^{\beta }}\backslash mu\_\{0\}=\backslash mu\_\{\backslash min\; 1\}\; e^\{-\backslash frac\{P\_\{c\}\}\{N\_\{i\}\}\}+\backslash frac\{\backslash mu\_\{\backslash max\; \}\backslash left(\backslash frac\{T\_L\}\{T\_\{0\}\}\backslash right)^\{-\backslash zeta\}-\backslash mu\_\{\backslash min\; 2\}\}\{1+\backslash left(\backslash frac\{N\_\{i\}\}\{C\_\{r\}\}\backslash right)^\{\backslash alpha\}\}-\backslash frac\{\backslash mu\_\{1\}\}\{1+\backslash left(\backslash frac\{C\_\{s\}\}\{N\_\{i\}\}\backslash right)^\{\backslash beta\}\}$$

• High-Field Mobility Model (Canali Model):

2.4 Interface Trap Model

• Exponential Tail Model:

  $$\mathrm{DOS}(E)=\frac{N_{trap}}{E_{tail}}{e}^{[-\frac{(E-E_0)}{E_{tail}}]}\backslash operatorname\{DOS\}(E)=\backslash frac\{N\_\{\; \{trap\; \}\}\}\{E\_\{\; \{tail\; \}\}\}\; e^\{\backslash left[-\backslash frac\{\backslash left(E-E\_0\backslash right)\}\{E\_\{\{tail\; \}\}\}\backslash right]\}$$

• Gaussian Model:

  $$\mathrm{DOS}(E)=\frac{N_{trap}}{\sqrt{2\pi }\sigma }{e}^{[-\frac{{(E-E_0)}^2}{2{\sigma }^2}]}\backslash operatorname\{DOS\}(E)=\backslash frac\{N\_\{\; \{trap\; \}\}\}\{\backslash sqrt\{2\; \backslash pi\}\; \backslash sigma\}\; e^\{\backslash left[-\backslash frac\{\backslash left(E-E\_0\backslash right)^2\}\{2\; \backslash sigma^2\}\backslash right]\}$$

2.5 Bulk Trap Model

• Shockley-Read-Hall Model:

  $$\begin{array}{c}{\displaystyle R_n^{tj}=c_{nj}n{N}_{tj}(1-f_{tj})-c_{nj}{n}_{1j}{N}_{tj}{f}_{tj}}\end{array}\backslash begin\{aligned\}R\_n^\{t\; j\}=c\_\{n\; j\}\; n\; N\_\{t\; j\}\backslash left(1-f\_\{t\; j\}\backslash right)-c\_\{n\; j\}\; n\_\{1\; j\}\; N\_\{t\; j\}\; f\_\{t\; j\}\backslash end\{aligned\}$$ $$\begin{array}{c}{\displaystyle R_p^{tj}=c_{pj}p{N}_{tj}{f}_{tj}-c_{pj}{p}_{1j}{N}_{tj}(1-f_{tj})}\end{array}\backslash begin\{aligned\}R\_p^\{t\; j\}=c\_\{p\; j\}\; p\; N\_\{t\; j\}\; f\_\{t\; j\}-c\_\{p\; j\}\; p\_\{1\; j\}\; N\_\{t\; j\}\backslash left(1-f\_\{t\; j\}\backslash right)\backslash end\{aligned\}$$ $$\begin{array}{c}{\displaystyle N_{tj}\frac{\mathrm{\partial }{f}_{tj}}{\mathrm{\partial }t}=R_n^{tj}-R_p^{tj}}\end{array}\backslash begin\{aligned\}N\_\{t\; j\}\; \backslash frac\{\backslash partial\; f\_\{t\; j\}\}\{\backslash partial\; t\}=R\_n^\{t\; j\}-R\_p^\{t\; j\}\backslash end\{aligned\}$$ $$\begin{array}{c}{\displaystyle c_{nj}={\sigma }_{nj}{v}_n={\sigma }_{nj}\sqrt{\frac{8kT}{\pi m_n}}}\end{array}\backslash begin\{aligned\}c\_\{n\; j\}=\backslash sigma\_\{n\; j\}\; v\_n=\backslash sigma\_\{n\; j\}\; \backslash sqrt\{\backslash frac\{8\; k\; T\}\{\backslash pi\; m\_n\}\}\backslash end\{aligned\}$$ $$\begin{array}{c}{\displaystyle c_{pj}={\sigma }_{pj}{v}_p={\sigma }_{pj}\sqrt{\frac{8kT}{\pi m_p}}}\end{array}\backslash begin\{aligned\}c\_\{p\; j\}=\backslash sigma\_\{p\; j\}\; v\_p=\backslash sigma\_\{p\; j\}\; \backslash sqrt\{\backslash frac\{8\; k\; T\}\{\backslash pi\; m\_p\}\}\backslash end\{aligned\}$$ $$\begin{array}{c}{\displaystyle \frac{1}{{\tau }_{nj}}=c_{nj}{N}_{tj};\frac{1}{{\tau }_{nj}}=c_{nj}{N}_{tj}}\end{array}\backslash begin\{aligned\}\backslash frac\{1\}\{\backslash tau\_\{n\; j\}\}=c\_\{n\; j\}\; N\_\{t\; j\};\; \backslash quad\; \backslash frac\{1\}\{\backslash tau\_\{n\; j\}\}=c\_\{n\; j\}\; N\_\{t\; j\}\backslash end\{aligned\}$$

• Gaussian Model:

  $$\mathrm{DOS}(E)=\frac{N_{trap}}{\sqrt{2\pi }\sigma }{e}^{[-\frac{{(E-E_0)}^2}{2{\sigma }^2}]}\backslash operatorname\{DOS\}(E)=\backslash frac\{N\_\{\; \{trap\; \}\}\}\{\backslash sqrt\{2\; \backslash pi\}\; \backslash sigma\}\; e^\{\backslash left[-\backslash frac\{\backslash left(E-E\_0\backslash right)^2\}\{2\; \backslash sigma^2\}\backslash right]\}$$

2.6 Impact Ionization Model

• Okuto Model:$$\begin{array}{c}{\displaystyle \alpha \left(F_{\text{ava }}\right)=a\cdot (1+c(T-T_0))F_{\text{ava }}^{\gamma }\exp [-{\left(\frac{b[1+d(T-T_0)]}{F_{\text{ava }}}\right)}^{\delta }]}\end{array}\backslash begin\{aligned\}\backslash alpha\backslash left(F\_\{\backslash text\; \{ava\; \}\}\backslash right)=a\; \backslash cdot\backslash left(1+c\backslash left(T-T\_\{0\}\backslash right)\backslash right)\; F\_\{\backslash text\; \{ava\; \}\}^\{\backslash gamma\}\; \backslash exp\; \backslash left[-\backslash left(\backslash frac\{b\backslash left[1+d\backslash left(T-T\_\{0\}\backslash right)\backslash right]\}\{F\_\{\backslash text\; \{ava\; \}\}\}\backslash right)^\{\backslash delta\}\backslash right]\backslash end\{aligned\}$$

3. Results and Discussion

3.1 Reverse Voltage Distribution

Figure 2. Potential Distribution in Super-junction VDMOS Device: (a) Equilibrium, (b) Reverse Bias 300V, (c) Reverse Bias 600V, (d) Reverse Breakdown

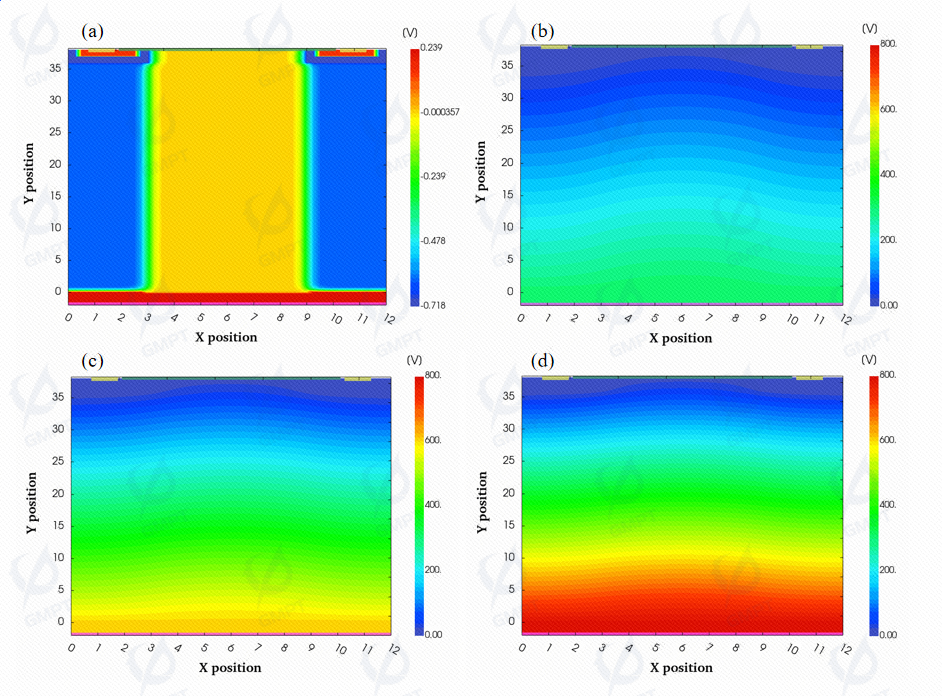
The figure above shows the potential distribution of the super-junction VDMOS device from equilibrium to reverse breakdown under reverse bias.

3.2 Reverse Breakdown Characteristics

Figure 3. Reverse Breakdown Curve of Super-junction VDMOS Device

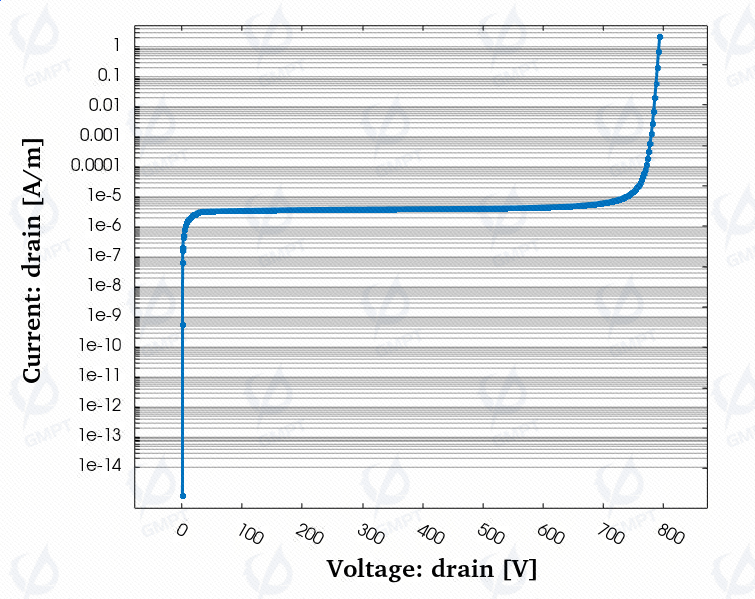
As shown in the figure, the drain current is approximately $5\times 10^{-6}A\mathrm{/}m5\backslash times\; 10^\{-6\}\; A/m$ before reverse breakdown, then sharply increases near the breakdown voltage due to avalanche breakdown, with a reverse breakdown voltage around 790V.

3.3 Threshold Voltage

Figure 4. Threshold Voltage of Super-junction VDMOS Device

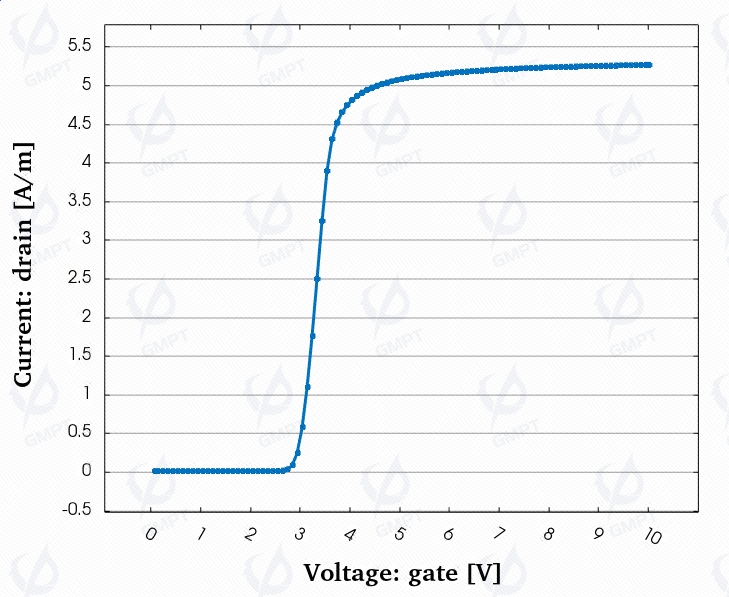
The threshold voltage of the super-junction VDMOS device is approximately 2.8V.

3.4 Transfer Characteristics

Figure 5. Transfer Characteristics of Super-junction VDMOS Device at Different Gate Voltages

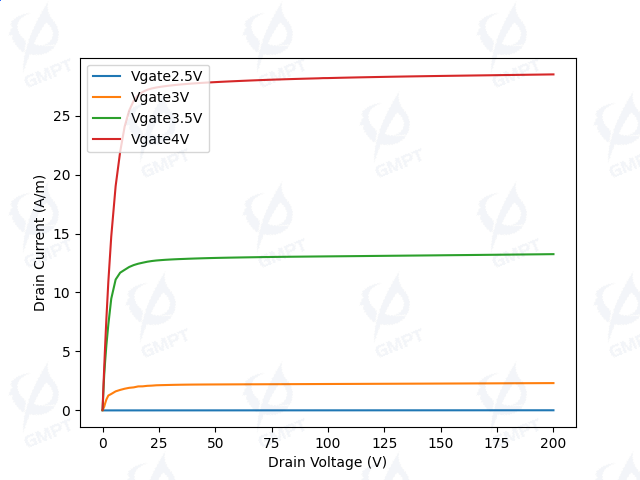
Figure 5 illustrates the transfer characteristics of the super-junction VDMOS device at gate voltages of 2.5V, 3V, 3.5V, and 4V. Since the threshold voltage of the device is 2.8V, the device channel is not open when the gate voltage is 2.5V, and there is no forward output. When the gate voltage exceeds the threshold voltage, the device channel opens, and the forward output increases with the gate voltage, while the drain current tends to saturate as the drain voltage increases.

4. Conclusion

This article presents the simulation process and results for a super-junction VDMOS device. It includes an introduction to the physical models applied in the simulation, along with key simulation results such as reverse voltage distribution, reverse breakdown characteristics, threshold voltage, and transfer characteristics under different gate voltages.

References

[1] Lyuqiang Li, "Process Window Improvement and Reliability Enhancement of Super-junction Devices," Master's thesis, University of Electronic Science and Technology of China.